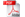The Role of Media in Emergency Management

Preface

Various kinds of incidents occurred more frequently in recent years. The 911 incident happened in 2001 was one of the social security incidents while "SARS" appeared in 2003 was attributed to the public health incident triggered by bacteria. There were other kinds of emergency that had made great tragedy on human beings such as the power blackouts in August 2003 in North America and tsunami natural disasters on Indian Ocean in 2005(Ji Lei, etc. 2006). Although the probability of all these incidents is very small, the influence is tremendous. For example on 26 December 2004 the Indian Ocean tsunami killed in excess of 225,000 people and dislocated millions more in countries spread around the Oceans rim from Kenya to Indonesia. The 2001 bombing of the World Trade Center in New York generated direct and indirect losses that most probably will exceed 50 billion US Dollars. Emergency incidents have become an important restricting factor for economic and social development.

There is increasing recognition of the need for study of emergency management. Some of the EM research relates to social sciences (Hughes, 1991). This type of research focuses on disaster results, sociological impacts on communities, psychological effects on survivors and rescue teams, and organizational design and communication problems (Li Jie,2005; C. S. ReVelle, H,2005;Swersey 1994, Sherali,1997). van Wassenhove wrote six cases on Humanitarian Logistics in Disaster Situations, commenting that "the subject of disaster management is an absolutely fascinating one that is growing in importance" (Van Wassenhove,2003). Green and McGinnis (2002) provide a discussion of the broad classification of these events by causation that helped frame our investigation. Others experts also gave details on classification of emergency in incidents management (Jean Luc Wybo, Harriet Lonka, 2002; Yang Jing, 2005; Eleftherios Iakovou, Christos Douligeris, 2001).

In reality, many countries and cities have established emergency response mechanism. USA established its Federal Emergency Management Agency (FEMA) in April 1979 which should be one of the earliest in the world. Many other countries also established related organizations and systems on emergency management, including Russia , Japan , South Korea , China , etc.

The Chinese government devotes great attention to disaster reduction and has achieved significant results. The Ministry of Civil Affairs of China assumes the work of organizing and coordinating emergency relief, supervising and promulgating information on disasters, managing and distributing disaster relief funds and central government materials and monitoring their use. The Ministry divides the work of responding to unexpected natural disasters into three grades based on the scene of disaster losses, and enacted the "Work rules for response to unexpected natural disasters of the Ministry of Civil Affairs of China" in June2003. China has promulgated laws such as the "Law on Flood Control of P. R. China" and "Law on Earthquake Control and Disaster Reduction of P. R. China"

Media has also played an important role as a social force except the government. Confronted with emergency, it's very important for the government to let the public correctly understand the current conditions and guide them to create a conductive atmosphere for solution to the incident through media. Therefore, media are indispensable in the process of emergency management. For example, during the early stage of SARS crisis, the medias of our country just try to deal with crises by attempting to prevent disclosure of uncomfortable facts. And this accelerates the spread of the diseases to some extent. In the critical time that the SARS crisis transformed from incubation to outbreak, however, all the medias changed their strategies and rush on the diseases information afterwards. Unfortunately the role of medias in the crises was very limited with lack of relative independence and failed to take the initiative to cooperate with the crisis management of government. In contrast, when the 9.11 incident broke, the medias delivers all kinds of news to audiences and guide them to act rationally, avoiding rumors spread effectively. Apart from discuss such problems about who was the terrorists and what actions the government would take, American media put their emphases on appealing the public to resume normal life as much as possible. Some newspapers even call on the public to refuel, shopping and spending. On the other hand, the over exposed scene of terrorists or slaughter about the 9.11 incident may result in panic. In one word, the news media plays an essential role in emergency management, but surveys indicate that the media is widely viewed as biased (Baron, David ,1845).

In our country the media always focus on positive publicity propaganda because of media constrain, and try to avoid to disclosure bad incidents because of strict control of the press. Is that effective to put medias in competitive market? In this paper we will discuss the factor of reducing media bias.

Assumption

We assume that readers hold biased beliefs, which might come from their experience, knowledge education, and previous news, or maybe just from prejudices. We assume that audiences prefer to hear or read news that is consistent with their beliefs. The idea that people appreciate, find credible, enjoy, and remember stories consistent with their beliefs is standard in the communications literature (Graber, Doris,1984; Severin, Werner and Tankard,1992). Research on information processing shows that people seek information that confirms their beliefs and to be less credible when confronted with data inconsistent with their beliefs (Klayman, Josh,1995, Rabin, Matthew and Schrag, Joel,1999).

Our second assumption is that medias have bias (Hayakawa, Samuel,1990). Bias could take a variety of forms. It could be ideological, where owners, editors, or journalists present stories that support particular world views. Bias could also result from information hidden or distorted by sources or because of personal preferences of journalists. Bias could also be measured in a variety of ways. For example, bias could be measured in terms of outcomes that differ from the average. Bias can be depicted in the following example. Suppose that another 4 suspect severe acute respiratory syndrome (SARS) case was identified. What are the different ways a paper can report this number? Consider just two different ways to presents the above fact.

Headline: SARS fears grow. New data suggest the SARS is growing severe. The Bureau of Health reports that the death number of SARA case increased by 4 again in the last week, and there are another 20 persons were diagnosed as suspect SARS case. This was an ominous sign of severity of SARS. It is only the beginning of more to come.

Headline: Turnaround in sight. Is the SARS poised for an imminent turnaround? Data from the Bureau of Health suggest that it might be. Newly released figures show death number of SARS case inching up just 4 in the last week compared with 8 persons died in the week before. That's because of the effective quarantine policy.

Neither story says anything false, yet they give radically different impressions. Each sounds reasonable, but each omits some aspects of the data: the first by neglecting to mention the death number of the week before, the second by ignoring the increased number of suspect SARS case. Each slants the news by not telling the whole truth, but they slant them in opposite directions. Our model of the market for news combines the assumption of readers preferring stories consistent with their beliefs, with the assumption that newspapers may slant stories toward beliefs. We examine two crucial aspects of this environment. First, we consider two alternative assumptions about the nature of competition: monopoly versus duopoly. Our model of media competition is analogous to a Hotelling model of product placement (Drew Fudenberg,1991; Jean Tirole1998). Newspapers locate themselves in the product space resembles to their reporting strategies. Audiences' beliefs determine their "transportation" costs since they spend psychic costs of reading papers whose reporting does not cater to their beliefs. In this context, our utility function implies quadratic transportation costs and our distribution of reader beliefs in the heterogeneous case corresponds to a uniform distribution of consumers.

Model Description and Analyses

Players: The players in our model are "media" and "audiences". The "media" may be the single organization in monopoly, or two corporations in competitive market, and "audience" is the potential reader of media.

Actions: "media" responses for emergency and announces its bias strategy s(d) and the price P it charges. Potential readers decide whether to buy the paper with the price P according to his belief.

Information: The media get some information about emergency incident. Because of the incomplete information and the constant variety, the media need to make some judgment by maximizing his expected utility.

3.1. Reader's Utility Function

Readers are interested in some underlying variable t which might come from their experience, knowledge education or previous news which is distributed N(0, v_t). Let p = 1/v_t denote the precision. Readers hold a belief about t that may be biased; beliefs are distributed N(b, v_t). We assume that a rational reader's utility is decreasing with the amount of slanting. So, if he reads a newspaper, his utility is:

Ur = u_i*(d)− Xs² − P

where P is the paper's price. If he does not read the newspaper, he gets utility 0.

Biased readers on the other hand get disutility from reading news inconsistent with their beliefs.

The distance between the news and the reader's beliefs, b, was measured as (n − b)². The overall utility of a biased reader is:

(1)                            U= u_i*(d) − Xs² −δ(n − b)²− P.

where δ> 0 denote his preference for hearing confirming news, u_i* (d)is the average function of i.

We consider two different distributions of reader beliefs, homogeneous and heterogeneous. Homogeneity means that all readers hold the same beliefs b. For example, all or nearly all Chinese believe that Taiwan is an indiscerptible part of China . Heterogeneity means that there is a distribution of reader beliefs. We assume that heterogeneous beliefs are distributed uniformly between b1 and

b2 where b1 < b2, and b₂>0. We denote by b* the average of b1 and b2.

In the homogeneous case, there is only one kind of reader. Bias is defined as the average amount by which the news read deviates from the data for the average reader, so we define B_hom = E_d[(n − d)²] to measures the average bias that readers encounter, where n is the news read by these readers. In the heterogeneous case, let n_i be the news read by reader i∈[1, 2]. Bias is then denoted as:

B_het = ∫_i E_d[(n_i − d)²].

3.2. Media's Strategy

Medias are in the business of reporting news about t. They receive some data d = t +ε. In the above example, these data might be the death number and the suspect SARE case. We assume that the medias then report these data with a slant s, so the reported news is n = d+s(d). Before seeing the data d, media announces its slanting strategy s(d) and the price P it charges. The media's utility function is (P-C)D, where D is the demand of readers. Potential readers decide whether to buy the paper with the price P. Once readers decide whether to buy the paper, the medias observes its signal d and reports n = d+s(d). Readers read the news and receive their utility.

3.3. Equilibrium in Monopoly market

Here we consider the equilibrium in two conditions. One is in monopolized market and the other is in competitive market. In the first condition we suppose there is a single media, and there are two medias in the second condition.

3.3.1. Confronted with homogeneous readers

Confronted with homogeneous readers, the media's can extract all surpluses in monopolized market. He maximizes expected utility:

max [u_i*(d) − Xs² −δ(n − b)²− C]=max u* −X ∫_d(s*(d)²) −δ ∫_d(d + s*(d) −b) ²-C

For a given d, differentiating with respect to s, then we can get:

Xs+δ(d+s-b-C)=0.

That is:

(2)                           S*_hom(d) =δ(b +C− d)/(X+δ)

Input the value of s to the expected utility, we get price P:

(3)                           P*_hom = u* −Xδ[b₂ + v_d] /(X+δ)

Then we can compute news he reports is:

n =δb/(X+δ)+Xd/(X+δ)

The reported news is a convex combination of bias and data, with weights given by utility parameters.

In this case we say the monopolist "slants towards b".

3.3.2 Confronted with heterogeneous readers

When confronted with heterogeneous audiences, the media's must first decide which one of the heterogeneous groups is its target audience when it comes to monopoly market.

Suppose medias faces a completely heterogeneous audience with b* = 0. For b*= 0, the monopolists profits equal to

(4)                          

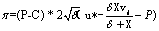
Let P_m be the global maximum of this function. At this maximum we get the boundary condition

(5)                         

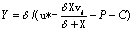
So if b2 − b1 < 2Y, the media will monopoly the whole market. He can then get maximum profits by setting a price equal to the utility of the boundary reader. His price and strategy is:

(6)                          s*_het =δ(b − d)/(X+δ)= −δd /(X+δ)

(7)                          P*_het = u* −Xδv_d /(X+δ) −δ²b2

If b2 −b1 > 2Y the monopolist chooses not to cover the market.

The media in monopoly market covers the market if the dispersion of reader beliefs is small enough. If beliefs are distributed too far apart, readers on either extreme will not read the paper.

3.4 Equilibrium in competitive market

We suppose there is two medias in competitive market and there are two different distributions of reader beliefs, homogeneous and heterogeneous.

3.4.1 Confronted with homogeneous readers

Case 1 In the competitive market, there are two medias confronted with homogeneous audiences. First we consider the price-setting stage with audiences is homogeneous. Let V_j be the reader's utility associated with reading news of media j. suppose V₁ > V₂, the price equilibrium is for media 1 to charge V₁ − V₂ and capture the full market, and media 2 get zero. If V₁ = V₂, then both medias charge C. C can be the fee for journalist or the opportunity cost for a reader to available to the media.

In the competitive market, the strategy of each media is holding constant the rival's strategy.

Any media's strategy is maximizing his expected utility:

max [u_i*(d) − Xs² −δ(n − b)²− C]

For both media, optimal strategy is:

(8)                         S*_hom(d) =δ((b +C− d)/(X+δ).

This shows that equilibrium is both medias provide equal utility, prices equal to C.

They show that, when audiences have homogeneous biases, competition does not eliminate them, it only leads to price reductions. Medias always cater to reader prejudices no matter in monopoly market or in competitive market. This means that we cannot get accuracy - even in the competitive media on information where the readers have similar beliefs.

3.4.2 Confronted with heterogeneous readers

When confronted with heterogeneous readers, the media's must first decide which one of the heterogeneous groups is its target audience in competitive market.

Firstly we calculate e the bias of the reader who is indifferent between reading the two media if media j charges P_j and has bias zj . This allows us to get the market share and the equilibrium price.

Secondly, we then calculate the best response functions for firms 1 and 2 respectively.

Suppose medias faces a completely heterogeneous audience with b* = 0 and we are in a symmetric situation where z_{2 =} - z₁, b₂ = -b₁. An audience with bias x receives utility:

u* −Xδ((v_d+e²)/(X+δ) −δ²(z_i− e)²/(X+δ) −P_j

from reading paper j. If the reader with bias x is indifferent between these two papers then their utilities are equal:

u* −Xδ(v_d+e²)/(X+δ) −δ²(z₂− e)²/(X+δ) −P₂₌ u* −Xδ((v_d+e²)/(X+δ) −δ²(z₁− e)²/(X+δ) −P₁

This equality can be simplified to:

(9)                     e= (z₁+ z₂)/2 + (P₂−P₁)X+δ/2 (z₂− z₁)δ²

Now we calculation best response price functions. Since the indifferent reader is located at x firm profits are given by:

π1= (P₁-C )(e-b₁)/(b₂-b₁)

π2= (P₂-C)(b₂- e)/(b₂-b₁)

Differentiate profits with respect to each price; we can get medias' best price response. For firm 1,

P1=P₂/2 +(b₂+z*)((z₂− z₁)δ²/(X+δ)+C

P2=(P₁-C)/2 +(b₂-z*)(z₂− z₁)δ²/(X+δ)

We get:

(10)                       P1=2(b₂+z*)((z₂− z₁)δ²/(X+δ)+3C/4

(11)                       P2=(2b₂− 2z*/3)((z₂− z₁)δ²/(X+δ)

The Nash equilibrium of market share can be calculated from the response functions:

e=z*/3-3C(X+δ)/8(b₂+z*)(z₂− z₁)δ².

Then we can calculate each medias' bias chosen by differentiating the profit function:

π1= P₁(e-b₁)

π2= P₁(b₂- e)

Differentiation with respect to z₁ gives:

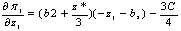
So Z₁*=3C/8-b₂ is bias equilibrium of media 1.Similarly bias equilibrium of media 2 is Z₂*= b_2－3C/8

Therefore Z₁*= 3C /8-b₂ and Z₂*= b₂-3C/8 is a Nash equilibrium.

Substitution the figure to profit function, prices must be equal to 4δ²b₂²/(X+δ).

Finally we verify that in equilibrium, the boundary conditions of the consumer are satisfied. That is we must show that:

u* −Xδv_d/(X+δ) −δ²(b₂+3C/8)²/(X+δ) − 6δ²b₂²/(X+δ)≥0

which equivalence to:

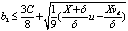
Now we get the medias choice in competitive market confronted with heterogeneous readers:

If,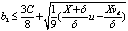

(12)                        

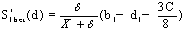
(13)                        

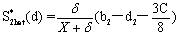
where without loss of generality we assume that firm 1 slants toward the left and firm 2 slants toward the right. They share the whole market. The opportunity cost C may affect the strategy of the media.

As in the standard Hotelling model, the media in monopoly market caters to both audiences unless they are too far apart, while medias in competitive market positions as differentiate from the other as possible and medias in monopoly market report more diverse news than in competitive market when readers are heterogeneous.

Conclusions

It was concluded that there are of no use to reduce bias in reporting to the median audience. Competition by itself is not a powerful force toward information accuracy. It forces newspapers to cater to the prejudices of their readers, and greater competition typically results in more aggressive catering to such prejudices as competitors strives to divide the market. By contrast, we found that audience diversity is a useful force toward accuracy. It is shown that the government should loosen the media constrain but not let go completely.

Firstly, our government should transit his mind and offer enough space to the media. Indeed, the media are an important force for the crisis management, which should not just be a speaker. Secondly the government should respect the "right to know" of the public and spurn the wrong opinion that open the disaster information to the public will lead to severe panic. Thirdly, establish information open constitution system to guarantee the information interaction smoothly and the right of media. The Government Spokesman institution offers an authoritative and credible source of information and proves to be effective in reducing media bias. Last but not the least, the media itself should also strengthen their sense of responsibility and raise the information quality to minimize the negative impact on emergency management.

References

1.   Baron, David, Persistent Media Bias, Stanford Graduate School of Business Working Paper No. 1845, 2004

2.   C. S. ReVelle, H. A. Eiselt, Location Analysis: A Synthesis and Survey, [J]. European Journal of Operational Research, 165(1), 2005, p.1-19

3.   Drew Fudenberg, Jean Tirole, Game Theory [M]. The MIT Press, 1991

4.   Eleftherios Iakovou, Christos Douligeris, An information management system for the emergency management of hurricane disasters, [J]. International Journal of Emergency Management. 2 (3/4), 2001, p. 243-262.

5.   Green, W.G., III, A development model for a statewide medical disaster response system, Paper presented at the National Disaster Medical System Conference, Las Vegas, Nevada, 2000

6.   Graber, Doris, Processing the News: How People Tame the Information Tide, New York : 33 Longman Press, 1984

7.   Hayakawa, Samuel, Language in Thought and Action, New York, NY : Harcourt, Brace & Company , 5th ed, 1990

8.   Hughes, M.A., A selected annotated bibliography of social science research on planning for and responding to hazardous material disasters, Journal of Hazardous Materials.27, 1991, p. 91-109

9.   Ji Lei, Chi Hong, Chen An etc Emergency Management, Higher Education Press.3, 2006, p. 93-94 (In Chinese)

10.  Jean Luc Wybo, Harriet Lonka, Emergency Management and the information Society: how to improve the synergy? International Journal of Emergency Management. 1(2), 2002, p.183-190

11.  Jean Tirole, The Theory of Industrial Organization, Cambridge, MA : MIT Press, 1988

12.  Klayman, Josh, Varieties of confirmation bias, The Psychology of Learning and Motivation. Vol. 32, Advances in Research and Theory. San Diego, CA : Academic Press, 1995

13.  Li Jie, Public Crisis Administration Institution for Public Crisis, [J]. Journal of Harbin University of Commerce: Social Science Edition. 1, 2005, p. 58-62 (In Chinese)

14.  Rabin, Matthew and Schrag, Joel, First Impressions Matter: A Model of Confirmatory Bias, The Quarterly Journal of Economics, 114(1), 1999, p. 37-82

15.  Severin, Werner and Tankard, James, Communication Theories: Origins, Methods and Uses in the Mass Media, New York : Longman, 1992

16.  Sherali, H.D., Brizendine, etc, Low probability high consequence considerations in routing hazardous material shipments, Transportation Science 31 (3), 1997, p. 237-251.

17.  Van Wassenhove, L.N., New interesting POM cases from Europe , POMS Chronicle 10 (2), 2003, p. 19

18.  Yamada, T., A network flow approach to a city emergency evacuation planning, International Journal of Systems Science 27 (10), 1996, p. 931-936

19.  Yang Jing, Chen Jianming and Zhao Hong, The Classification of Emergency in Incidents Management, Management Review. 4, 2005, p. 37-41 (In Chinese)