Evaluation Methods of The Text Entities

Introduction: Concepts and Definitions

In (Marius Popa, 2005), (Ivan, Popa, 2005), (Ivan, 2003), (Ivan, Popa, Boja, Toma, 2005, 43–57) some concepts used in building, analysis and evaluation of the text entities  are defined and presented. The used concepts include the following elements: alphabet, word, vocabulary, subvocabulary, text, template, structured text, entity.

For each used concept, it is offered a definition, the necessity of its using, its characteristics, using forms, ways for information representation through its using, models, requirements and examples of building and using.

Through defined concepts, it is highlighted some representation and structuring forms of data. The data quality is given by the level assured for quality characteristics associated to data. The identification and quantification of data quality characteristics are critical activities in control and assurance processes of the quality.  

According to definition from (Marius Popa, 2005), the text entities are constructions formed by word strings characterized by word positions in text, word grouping in order to define a context, by correspondence of the words with elements, actions and phenomenon from real world, qualitative attributes that group concrete aspects from real world in homogenous collectivities in connection with established criteria.

In (Ivan, Popa, 2005), the conditions that must be respected in building process of the text entities are established. These ones look upon the following aspects:

·         A strong delimitation of the approached domain;

·         Key word definition for the domain;

·         Vocabulary used, that also includes the key word vocabulary;

·         Concepts, techniques, methods, methodology and technology knowledge for the domain;

·         Detail and other domain connected element documentation;

·         Respecting of syntax rules for each language;

·         Rules to be followed, regarding entity structuring, progressive approaching of the problems, usage of standard formats to represent the text information.

In (Department of Defence 8320.1-M, 1994), in accordance with Federal Information Processing Standards from United States of America, the data quality is defined as accuracy, opportunity, completeness, importance and accessibility that make data to be appropriate, that is to be corresponding with its usage.

Data quality includes the activity and data model usage, entities, attributes, metadata, diagrams and data architectures.

The text entity quality ET is given by  all features that the entity have. These ones are perceived and appreciated by the persons whom are part of a group. In comparison with an evaluation system, appropriate for each person, the text entity ET has associated a score, a mark that differentiates it of other text entities or includes it in a collection (Ivan, Popa, 2005).

Evaluation Formulae

Aspects regarding the model development associated with evaluation metrics of the text entity quality characteristics are presented in (Popa, 2005), (Ivan, Popa, 2005), (Ivan, 2003), (Ivan, Popa, Boja, Toma, 2005, 43–57.

The evaluation metric building of text entities leads to text quality evaluation system making. The metrics included in this system are structured in two classes function of complexity classes of the used concepts as result of their aggregation:

·         Quality characteristic metrics developed on the base of structure and semantic content of text entities;

·         Metrics of the data representation form on the base on a representation reference system.

In first category of metrics, in (Marius Popa, 2005) metrics regarding the volume and dynamics of data, correctness, completeness, reliability, complexity, comparability, homogeneity and orthogonality of text entities were developed. It remarks as importance the sub-category of metrics developed in order to measure the orthogonality.

In the second metric class, there are included the quantification models for fundamental syntactical construction orthogonality used for text entity building. These constructions aim: symbol, character and word.

In (Marius Popa, 2005), a reference system is defined in order to represent the symbols from the alphabet. Metrics for the alphabet internal orthogonality evaluation are developed and also metrics associated to the orthogonality among alphabets.

In order to determine the orthogonality between two symbols a_i and a_j of a alphabet, it is built the metric H(a_i, a_j). A main importance to make conclusions regarding the whole alphabet symbol orthogonality is given by aggregated indicator computation with the following analytical form (Marius Popa, 2005):

where n represents the symbol number of the alphabet.

In the same category of metrics, there are include the metrics that measure the word orthogonality. Thus, there are determined the words that are part of the same word family, identifying the words with the same root. In (Marius Popa, 2005), methods and models form word family identification are presented. Also, aggregation processes of the primary indicator values are implemented.

In the most part of the cases, the indicator aggregation is made by geometrical mean using. This thing is favoured by the fact that the orthogonality indicator values can be structured on two dimensions, what leads to a metric with the following analytical form:

where:

g_f – aggregated metric for orthogonality evaluation;

- value number resulted from orthogonality metric applying among different text constructions;

g_pi – primary metric for orthogonality evaluation.

On the base of aggregated metrics, conclusions regarding the characteristic for the whole collectivity are obtained.

Evaluation Algorithms

Using of a text entity evaluation metric doesn’t suppose anytime only the proper model using, but requirements assurance for the input data.

The bigger complexity of the models associated to text entity evaluation metrics determines the algorithm development for input data preparing, model implementation and post-evaluation operations to permit a big accuracy interpretation of the characteristics measured by metric.

Thus, in (Marius Popa, 2005), (Ion Ivan, Daniel Milodin, Marius Popa, 2005, 41–56) there are developed and implemented algorithms for implementation of the models associated to text entity metric. For example, for metric quantification H(a_i, a_j) regarding two symbol orthogonality from an alphabet the following algorithm was developed and implemented:

P1: it is defined a reference system formed by the segments s₁, s₂, ..., s_ns used to build each symbol from the alphabet;; ns represents the segment number from considered reference system.

P2: it defined a reference rule of the reference system segments.

P3: it associates a rank r_i for each segment s_i from reference system, obtaining the pairs (s_i, r_i).

P4: it represents the alphabet symbols, using the reference system.

P5: it builds a matrix M(A_L) such as the element m_ij = 1 if to build the symbol a_i from the alphabet A_L it uses the reference segment s_j. If the reference segment s_j is not used then m_ij = 0.

P6: it computes the sums on columns, S_j, to obtain the using frequencies of the segments from the reference system in symbol defining from the alphabet.

P7: it computes the maximum and minimum sums, S_max and S_min.

P8: it normalizes the values S_j on the base of the expression:

The values Sn_j are included in [0; 1].

P9: it interchanges the columns of the matrix M(A_L) to obtain an ascendant order for the values Sn_j.

P10: it makes the correspondence of the values Sn_j with the segments s_j from the chosen reference system.

P11: it re-codifying the ranks of the reference system such as the new numbers to highlight the using frequencies, obtaining the pairs (s_j, ).

The presented algorithm is a rigorous way to evaluate the orthogonality of the symbol representations in an alphabet. The symbol representation orthogonality increasing has importance and use in building process of the text entity with symbols good differentiated.

Evaluation Software

The determination through a software application of the quality characteristic values and text entity orthogonality metrics suppose the carrying on of the following activities:

·         Application objective definition;

·         Input establishment on the base of quality characteristic system and metric model study.

·         System architecture building;

·         Collecting, normalizing and organizing of the data in correspondence with metric requirements;

·         Metric system implementation;

·         User interface designing in assistance of the process to establish the text entity base orthogonality;

·         Metric system testing, tracing the software product behavior in limit cases especially.

In (Marius Popa, 2002) is presented the architecture and function of the product Cloning Analysis Software – CAS. This software application implements the metrics for the fundamental characteristics for texts and data organized in matrixes. In figure 1, there are highlighted the modules of CAS application.

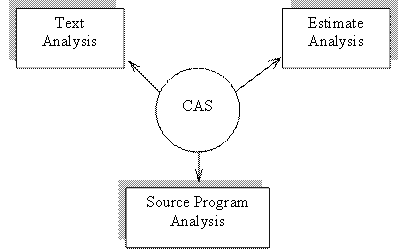
Figure 1 The modules of CAS application

The text orthogonality analysis from the text entity base supposes the building of aggregated orthogonality indicators matrix for the text entity pairs.

The orthogonality aggregated indicator associated to entity pair is obtained through orthogonality determination for the following primary metrics, (Marius Popa, 2002): entity length, appearance frequencies of the alphabetic characters, user vocabulary, text entity vocabulary, common vocabulary, the entity structure.

In the quantitative analysis of the estimates, the used algorithms for orthogonality aggregated indicator suppose the following step passing:

a.       Data structure initialization loaded with data about estimates;

b.      Data loaded regarding the estimate structure and their content;

c.       Derived value determination;

d.      Comparison of primary and derived values;

e.       Orthogonality aggregated indicator determination.

The source program orthogonality analysis from the project annexes of the text entity bases supposes the building of the aggregated orthogonality indicator matrix. The aggregated indicator is obtained through the following primary metric determination, (Marius Popa, 2002): program length, appearance frequencies of the alphabetical characters, user vocabulary, program vocabulary, common vocabulary, entity structure, defined variables, precedent matrix of the variables, variable position.

In (Marius Popa, 2005), there are presents the application characteristics of Bibliography Analysis – BA that performs regarding: appearance frequencies of the syntactical constructions, file structuring, measuring of the word finding degree, key word searching, bibliography elements processing. The application offers to the user some aggregated indicators regarding the analyzed elements.

Software automatizes the evaluation process of the text entity quality, a very important aspect in their qualitative analysis.

Testing Examples

It considers the Slav alphabet A_S and Greek alphabet A_G. The internal orthogonality indicator evaluation algorithm depending of representation way, there are obtained values structured in a matrix structure.

Thus, the appearance matrix of the values for symbol pair orthogonality of the Slav alphabet is presented in table 1.

Table 1

The frequencies of the orthogonality for the alphabet A_S

The values of the orthogonality levels for symbol pairs from the Greek alphabet are highlighted in the following table:

Table 2

The frequencies of the orthogonality for the alphabet A_G

The symbol representation is made on the base of the reference system from (Ion Ivan, Daniel Milodin, Marius Popa, 2005, 41–56). In (Ion Ivan, Daniel Milodin, Marius Popa, 2005, 41–56), a comparative analysis of the alphabet orthogonality is made on the base of the values included in matrixes with the orthogonality values appearance frequencies.

The aggregated values of the internal orthogonality of the two alphabets are given in table 3.

Table 3

Alphabet orthogonality indicator values

The orthogonality analysis permits the alphabet design that increases the orthogonality. The character representation orthogonality increasing is important because the symbols from the alphabet have a better differentiation.

Conclusions

The paper highlights some techniques and methods for text entity evaluation. The emphasis is on orthogonality characteristic that allows the qualitative improvements in building and evaluation processes for the text entities.

The software products have a plus of efficiency in order to get to proposed objectives, and the testing examples contribute to proposed algorithm and developed software application validation

References